Además de los modelos matemáticos y físicos del marrón,
existen más conocimientos que recopilamos en este capítulo.
11.1. Teoría del Trabajo y el Dinero (por qué tu jefe gana
más que tú)
Después de arduas averiguaciones hemos conseguido dar con un estudio matemático
que explica por qué tu jefe siempre gana más que tú, aunque siempre curre menos.
Partiendo de dos premisas básicas que son:
CONOCIMIENTO es PODER y TIEMPO es DINERO,
se obtienen las siguientes ecuaciones:
(1) Conocimiento = Poder
(2) Tiempo = Dinero
De las leyes de la física sabemos que:
(3)
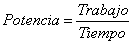
y Potencia (del ingles) = "Power" = PODER
Sustituyendo en (3) según las ecuaciones (1) y (2) Poder por
Conocimiento y Tiempo por Dinero resulta entonces que:
(4)

y finalmente, aislando dinero nos queda
(5)
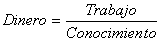
Analizando la ecuación (5) podemos ver que a medida que conocimiento
tiende a cero, Dinero tiende a infinito.
Conclusión:
| Cuanto uno menos sabe, mas gana |
Nota a la ecuación (5):
También es cierto que si mantenemos el conocimiento constante, cuanto más
trabajo más dinero... pero claro eso solo es cierto matemáticamente, y al
igual que los números imaginarios, no tiene sentido físico real...
De hecho, al aumentar el trabajo suele aumentar nuestra experiencia y por
tanto el conocimiento, con lo que el dinero permanece constante, y nuestro
cabreo en aumento.
De lo que se deduce el 1er
Postulado de Brown
1er Postulado de Brown
| La mejor forma de conseguir ganar más dinero en el trabajo es ser
incapaz de aprender de la experiencia |
En el caso contrario, si aprendemos
de la experiencia y llegamos a hacerlo todo bien, nuestro jefe quedará encantado
y nos mantendrá en el mismo sitio para siempre, anulando nuestra posibilidad
de ascenso de por vida.
De la expresión (4) también se puede
deducir esta otra:
(6) Trabajo = Conocimiento
* Dinero
De lo que se puede deducir el siguiente corolario
Corolario
| Ya que el dinero suele ser constante, cuanto más conocimiento tengamos
sobre algo, mayor será el trabajo que nos caerá encima |
De esta afirmación se puede deducir el 2º Postulado de Brown
2º Postulado de
Brown
| La forma más efectiva de evitar los marrones es ser demostradamente
incapaz de resolverlos |
Hemos de tener en cuenta que este
Postulado se da en la situación de que la cantidad de dinero sea constante,
ya que si no, corremos el riesgo de que al disminuir el conocimiento acabemos
en la puñetera calle, por listos.
Estas leyes han resultado ser ciertas
en la práctica. De todos es conocido el caso del becario que trabaja
más que nadie por cuatro duros (doce céntimos de euro) y del jefe
que se pasa todo el tiempo reunido o fuera de la oficina y gana cada mes tanto
como tú en un año.
Por otro lado, y como consecuencia
del Principio de Peter, los jefes están más cerca de llegar, si
no han llegado ya, a su nivel de incompetencia, lo que equivale a una falta
de conocimiento para resolver sus tareas cotidianas. Esto explica claramente
por qué han de cobrar más.
11.2
Estudio del becario de chicle
Mucha gente cree que los becarios
se pueden estirar y estirar como si fueran un chicle, de forma que resuelvan
el trabajo de varios proyectos, haciendo
labores de titulados superiores y ganando una miseria.
La verdad es que los becarios de
chicle, como todo buen PBC, son sufridos y trabajadores. A continuación
incluimos un problema de examen de Organización del Trabajo, en el que
se ilustra el comportamiento de estos sujetos.
Problema de examen de Organización
del Trabajo
Sea un becario de chicle, que se
quiere repartir entre dos proyectos dados. Estos proyectos no tienen presupuesto
suficiente para pagar un becario cada uno, por lo que lo tienen que compartir.
a) Hallar el límite de elasticidad
del becario.
El límite de
elasticidad es aquel en el que el objeto se deforma tanto que ya no es capaz
de recuperar su forma anterior.
Para un becario
estándar de media jornada (contrato por 4h diarias) el límite suele estar en
torno a las 8h diarias, suponiendo que además tiene que ir a clase y preparar
los exámenes.
b) Hallar el límite
de ruptura del becario.
El límite de ruptura es aquel en el que el objeto se rompe definitivamente
y se divide al menos en dos trozos. Suele ocurrir cuando al objeto se le somete
a una excesiva tensión.
Supondremos que los dos proyectos tiran del becario con igual fuerza, para
que la tensión sea máxima y se provoque antes la ruptura.
El límite de ruptura se obtiene cuando se supera uno o más de los valores
normalizados editados por el ITU-B en la tabla “Resistencia típica del PBC”
Los valores típicos a aplicar en este caso son los siguientes
- 10h diarias, para un becario estándar de media jornada
- 15h diarias, para un becario de jornada completa.
- 50.000 ptas (300 € ) para un becario de jornada completa.
A estos valores hay que realizarles las siguientes correcciones:
- Aumentar 1 h en caso de ingenieros
- Aumentar 1 h si se dedica a programar
- Aumentar ½ h si tiene derecho a comer en el comedor de la empresa (suele
ser algo mejor que el de la facultad y les ahorra tiempo)
- Disminuir 10.000 Ptas. (60 €) por cada curso completo que le quede para
acabar la carrera.
c) Hallar el
punto óptimo de corte del becario, para repartirlo entre los dos proyectos
Teniendo en cuenta la aversión natural de los becarios a cualquier elemento
que atente contra su integridad física, será muy dificil dividir al becario
físicamente, por lo que la división deberá ser en el tiempo.
Si suponemos el becario típico de media jornada, y teniendo en cuenta sus
restricciones de disponibilidad temporal, lo mejor es que esté media jornada
(por ejemplo por la mañana) en un proyecto, y la otra media jornada (pongamos
por la tarde) en el otro proyecto, pero con disposición para ayudar en el
primer proyecto cuando sea necesario al acabar su jornada laboral. En la media
hora de la comida deberá disponer de tiempo para estudiar las fotocopias
de los apuntes de las clases a las que no pudo asistir por estar "trabajando"
y elaborar las memorias de las prácticas de laboratorio a las que no
pudo asistir.
|

