Durante mucho tiempo, estudiosos de todo el mundo han intentado explicar de una forma
científica el comportamiento de los marrones.
La cruda realidad es que en cuanto lo intentaban, los pobres se veían inmersos en un
gran marrón, dada la dificultad del tema y lo complejo de su experimentación.
Además, siempre han escaseado voluntarios para experimentar sobre ellos, y los pocos
que se prestaban, al final no eran capaces de aportar nada positivo sobre el objeto en
estudio.
En la actualidad, el BMG ha recogido la dispersa bibliografía que existe referente al
tema con el fin de establecer de una vez por todas la Teoría Unificada del Marrón,
gracias a la cual se espera poder predecir el comportamiento de los marrones en general.
No hace falta decir que ha sido una ardua tarea. En esta labor investigadora, lo más
difícil siempre ha sido el quitar la cantidad de porquería que había sobre los pocos
manuscritos existentes.
9.1 Cálculo de la probabilidad de asignación de marrones
A fin de ayudar a lector a evitar en la medida de lo posible la afluencia de marrones
sobre su persona, incluimos a continuación un método para calcular la densidad de
probabilidad de llevarse un marrón a cuentas, en un momento dado.
El siguiente teorema es fruto de los sesudos esfuerzos de los profesores Johnnie
Esparzin y Julius Brown de la prestigiosa Universidad de Brownachussetts (La Moraleja,
USA).
La densidad de probabilidad de llenarse de caca (Pkk) en un lugar de trabajo
responde a la siguiente expresión:

donde:
| Factor |
Descripción |
Unidades |
F: |
Factor de corrección de Fakin-Vossman, que depende
básicamente del ángulo de visibilidad que tenga el jefe de tu sitio. Este factor incluye
así mismo correcciones sobre el grado de inesperabilidad del marrón, que hacen tender el
valor del factor a 1. |
adimensional |
P |
Prisa del abnegado trabajador por salir ese día. |
hurrys |
Bt |
Constante de Factores Medioambientales. Esta constante tiende
a infinito cuanto mejor está el día. |
güeters |
Oc |
Nivel de Ocupación del trabajador. |
busys |
In |
Media estadística de la densidad de probabilidad de la
función de Inutilidad del marrón esperado. |
|
Ts |
Constante directamente proporcional al tiempo que resta
teóricamente para tu salida de la empresa. Cuanto menor sea este tiempo, mayor será la
probabilidad de browning. |
segundos |
Sobre el factor de corrección de Fakin-Vossman, hay que tener en cuenta que se compone
de varios términos:
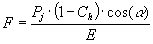
donde:
| Factor |
Descripción |
Unidades |
Pj |
Probabilidad de que te encuentre el jefe. Este factor depende
de la distancia a la Brown Zone más próxima y de la movilidad relativa del jefe. |
adimensional |
Ch |
Capacidad de huida. Este parámetro es inversamente
proporcional a lo lejos que esté la salida. Evidentemente, Ch << 1. |
runaways |
a |
Angulo con el que el jefe ve tu mesa según sale de su
despacho. |
grados |
E |
Esperabilidad del marrón. |
ingenuitys |
Notas sobre la expresión:
la mayoría de los parámetros que intervienen en la expresión de Braunin-Esparzin son
de difícil cuantificación y en su mayoría son fruto de cuidadosos procesos de medida.
Así, la experiencia dicta que la probabilidad de que te encuentre el jefe (factor Pj
de Fakin-Vossman) es siempre mayor que 0.5.
Existen tablas empíricas que ofrecen los valores de estos parámetros. Estas tablas
están recogidas en el informe I-666 del ITU-B: "Browning parameters for the face:
An empirical approach". Entre estas tablas se encuentra las tablas de corrección
de Brownfinni, que corrigen algunos de los parámetros anteriores en base al valor de
otros.
En lo que respecto al parámetro Ch, no se tiene constancia de que Ch
pueda ser igual a 1. El lector deberá suponer siempre que Ch Î [0, 1).
Para el factor de esperabilidad, E, tan sólo se han podido realizar cálculos de tipo
empírico. Estos cálculos se han basado en la observación del grado de felicidad de los
incautos futuros browned. Se puede observar claramente en la expresión de
Fakin-Vossman que 1 runaway = 1 ingenuity, con lo que F es adimensional.
Un último detalle es que el lector avispado habrá podido observar que la fórmula de
Braunin-Esparzin puede dar lugar a probabilidades de comida de marrón mayores que 1.
Esto, que parece contradecir toda la teoría clásica de estadística, no es más que un
efecto relativista debido a la velocidad con que se suelen generar los marrones. Los
marrones no se generan a c (velocidad de la luz), pero muchas veces van a 0.9c.
El resultado de este molesto efecto (denominado efecto Brown-Warp) es que el sujeto
pasivo del marrón no se comerá uno, sino varios marrones simultáneamente.
Ejemplo práctico:
Sea un trabajador A, que se encuentra cómodamente situado en una mesa en forma de L a
unos 10 metros de la salida más próxima de la sala en que se encuentra. Es viernes, 24
de mayo, y hace una tarde fenomenal (27º y sin nubes. Ligera brisa). Nuestro currante, A,
ha quedado con su novia a las ocho de la tarde para ir al cine y luego a cenar. Son las
seis menos cinco de la tarde y A ha trabajado duro para tener listo encima de la mesa del
jefe el último informe urgentísimo sobre la exportación de margaritas de siete pétalos
(famosísimas porque siempre contestan que sí) a Mozambique. Al lado de A se sienta otro
trabajador, B, que tiene tres años de antigüedad en la empresa más que A y que lleva
toda la tarde escribiendo extrañas misivas sin moverse ni levantar la vista de la mesa.
Teniendo en cuenta que el despacho del jefe de A se encuentra a unos 15 m de su mesa y
hay visión directa (30º) entre él y A, y que es de sobra conocida la afición de dicho
jefe por retocar los documentos ("Pues este párrafo me lo pones en negrita, esta
tabla en gris y este título en rosa fosforito..."), calcule la probabilidad de
que la novia de A se vaya al cine con B.
Solución:
Este es un caso claro en el que aplica el Teorema de Braunin-Esparzin.
El primer paso es obtener el valor del Factor de Fakin-Vossman.
Dado que existe visión directa entre el jefe y A, la probabilidad de que el jefe
encuentre a A es directamente mayor que 0.5. Aplicando la tabla de corrección por
distancia de Brownfinni tenemos que:
Pj = 0.8
Por otro lado, dado que A se encuentra a 10 m de la salida más próximo es evidente
que el factor Ch será digno de consideración. Sin embargo, el hecho de que su
mesa sea en forma de L obstaculiza la posible huida en función de la postura que esté
adoptando A cuando el jefe se levante de la mesa; en estos casos, la práctica aconseja
asignar a Ch un valor entre 0.4 y 0.3. Poniéndonos en el caso peor, sea:
Ch = 0.3
Por último, en lo que respecta al factor de esperabilidad, es obvio que A no piensa en
otra cosa que salir de allí, lo que reduce el factor. Pero teniendo en cuenta la actitud
sospechosa de B, A podría llegar a mosquearse. Esto, sumado a la experiencia acumulada de
A en marrones en su empresa, nos permite concluir que la esperabilidad del marrón es del
50%, o sea 0.5 ingenuitys.
Con todo, el factor de Fakin-Vossman resulta:
F = (0.8·0.7·cos30) / 0.5 = 0.96
Veamos ahora el resto de parámetros de la expresión. Es obvio que habrá que
aproximar algunos de los valores. En particular es obvio que la media de la función de
inutilidad del trabajo es 1. A nuestro estimado currante no le cabe duda de ello. Por otro
lado, el enunciado dice que el trabajo está terminado, por lo que a A tan solo le quedan
por hacer algunas cosillas de última hora y recoger la mesa; puede suponerse sin cometer
mucho error que está a 0.1 busys de ocupación. Ts es de 300 segundos.
La prisa de A por salir de allí es bastante alta, pues su novia le ha hecho saber
reiteradamente que esta harta de quedarse sola en casa esperando a que salga del trabajo y
que como no espabile él verá. Esto hace que su nivel de prisa sea de 60 hurrys (véase
la tabla 1437.23 del I-666 del ITU-B). Por último, la tarde es espléndida. Consultando
las tablas temporales del I-666 del ITU-B, en el cruce de la columna del 24 de mayo con la
fila de 27 grados (Celsius) resulta un Bt de 173.7 güeters (ya corregido con
el modificador de brisa ligera).
Con todo ello:
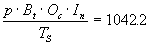
de donde:
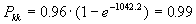
Lo que nos permite concluir que A ya puede ir pensando en hacer una visita a la
cafetería de "Lo que necesitas es amor"
"La función de asignación de marrones es continua pero no derivable en el
intervalo (0, ¥ ) y presenta un máximo absoluto en el punto donde la pendiente de la
curva de despiste se hace infinita"
Lo que traducido al vulgo viene a decir que si no tienes nada que hacer y se te nota
estás jodido.
La no derivabilidad de la función implica, además, que las técnicas de swapping
no son realizables en este caso.
9.3. Propiedad asociativa del marrón
"Un marrón nunca viene solo"
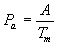
donde:
| Factor |
Descripción |
Unidades |
Pa |
Probabilidad de aparición del siguiente marrón |
adimensional |
A |
Amplitud del último marrón comido |
brownies |
Tm |
Tiempo transcurrido desde el último marrón |
segundos (sí, sí) |
NOTA: Esta función no es finita en el instante cero e indica la alta
probabilidad de que te cuelen varios marrones de una sola vez.
"El grupo de los marrones forma un espacio vectorial de color castaño oscuro
definido sobre el cuerpo de los complejos"
Sobre este espacio se definen una serie de propiedades que serán muy útiles a todo
tipo de Browneds para saber cuales son las reglas por las que se rigen los mismos.
Para construir este espacio vectorial se definen las siguientes operaciones:
9.4.1. Suma de marrones
La suma de marrones tiene las siguientes propiedades:
No es una operación lineal
La suma de dos marrones NO es igual a la suma de sus amplitudes
Para calcular un marrón suma de otros dos se debe utilizar la siguiente fórmula:
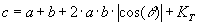
Donde:
a y b son dos marrones que se
suceden en el tiempo.
q es el ángulo de incidencia del marrón b sobre el a.
Kt es una constante temporal que aumenta con lo
avanzado que se lleve el trabajo de a cuando aparece el marrón b
Nótese que se toma el valor absoluto del Cos(q ), ya que en ningún caso se puede
considerar negativo este término. Además, cuando a es totalmente independiente de
b, el ángulo vale p /2 y el coseno vale cero. En cambio, si b incide directamente
sobre el trabajo de a, o es totalmente opuesto, el marrón desencadenando por la
interacción de los dos es tal que rezarás para que no te pille cerca.
Evidentemente la suma de los marrones depende del orden en que lleguen. Esto demuestra
por un contraejemplo:
Si estás liado un marrón pequeñito (al que ya te has comprometido) y te cuelan El
Gran Marrón, te comes los dos. En cambio si primero te cuelan El Gran Marrón, ya no
pueden colarte ningún otro de tamaño menor, conclusión: sólo te comes uno. Resultado:
Te enmarronas hasta las cejas en cualquiera de los dos casos, pero el primero es todavía
más grave.
Corolario: Intenta asignarte un buen marrón (o uno que lo aparente) si prevés
una buena lluvia de marrones (no hay mejor forma de evitar que te mojen que el ya estar
mojado)
- Es asociativa en el Espacio Vectorial de los Marrones
"Dado un número n de marrones, da igual el orden en que los agrupes: te los
comerás todos por igual".
La propiedad asociativa arriba enunciada se cumple, pudiéndose calcular la
probabilidad de dicha asociación con el método explicado antes.
Algunas características de la propiedad asociativa son las siguientes:
- Los marrones pequeñitos siempre llevan asociado uno grande. Un claro caso de ello es
cuando te cuelan un marrón para hace una estimación de un trabajo. ¡Peligro!
Tienes todas las papeletas para que te toque a ti hacer el trabajo, que a buen seguro
será un buen marrón.
- Los marrones grandes, sobre todo si tardan mucho en acabarse, crean asociaciones con los
marrones de alrededor, de forma que al cabo de un tiempo forma una gran plasta marrón que
salpica a todo el mundo.
- Las asociaciones entre marrones surgen espontáneamente y dan lugar a nuevos marrones.
Este hecho viene producido por las interacciones no deseadas entre los distintos marrones,
que generan tareas de coordinación, resolución de incompatibilidades entre versiones,
aclaraciones de malentendidos, etc. . .
9.4.3. Multiplicación de marrones
"Creced, multiplicaos y dominad la Tierra... " (Revisión del Génesis
según Johnnie Esparzin, Capítulo II, versículo 4)
La multiplicación de marrones en realidad encierra dos operaciones: el producto
vectorial de marrones (multiplicación de marrones entre sí) y el producto escalar,
definido sobre el cuerpo de los complejos (multiplicación de un marrón por un número)
Producto vectorial de marrones
La multiplicación de marrones (o producto vectorial) es una de las situaciones más
desastrosa a la que se puede enfrentar cualquier mortal. Si encima eres un browned
de nivel bajo, estás perdido.
Consiste en que a partir de dos (o más) marrones linealmente independientes se
empiezan a generar nuevos marrones como consecuencia de las interacciones entre ellos. (A
este efecto también se le denomina generación de productos de intermarronación)
No hay que confundir una situación de multiplicación de marrones con una lluvia de
marrones. En el caso de la lluvia, los marrones aparecen de forma independiente y por
generación espontánea y en el de la multiplicación aparecen como combinación de otros
previamente existentes.
El número de marrones generados en una multiplicación de marrones se calcula por
combinatoria y es igual a las variaciones con repetición de "m" elementos
tomados de "n" en "n", donde:
m es el número de marrones inicial
n es el número de marrones que salen de la primera hornada. este es un valor
que se ha de obtener a posteriori, ya que es muy difícil de adivinar.
El hecho de que las variaciones sean con repetición responde al hecho de que en estas
situaciones se suele mandar lo mismo varias veces y a varias personas distintas.
9.4.4. Producto escalar de marrones
La multiplicación de los marrones por un número afecta directamente a la cantidad de
marrones y a su intensidad. Así, al multiplicar un marrón por 2 podemos estar obteniendo
un marrón del doble de intensidad o dos marrones de igual intensidad que el primero.
¡También puede darse el angustioso caso de que obtengamos dos marrones del doble de
intensidad!
Esta imprecisión en el resultado final viene dada por la no linealidad del espacio
vectorial y de la existencia de agujeros negros en el mismo. (Agujeros marrones, más
bien)
El caso es que la operación de la multiplicación se define no sólo sobre los
números reales sino también sobre los complejos. Recordemos que un número
complejo es aquel que tiene una parte real y otra imaginaria. Pues bien, si multiplicamos
un marrón por un número complejo obtendremos un marrón con parte real (lo que realmente
hay que hacer) y una parte imaginaria (lo que se imagina el jefe que hay que hacer, pero
que no es real – ni hace p... falta hacerlo).
La proyección de los marrones sobre el cuerpo de los complejos explica por qué un
marrón real acaba teniendo partes imaginarias que realmente rayan la ciencia-ficción.
Todo es un producto de la calenturienta imaginación de algún browner durante el
ciclo de vida del marrón.
- Propiedad distributiva respecto de la suma
En un espacio vectorial clásico la propiedad distributiva de la multiplicación
respecto de la suma dice que:
a*(b+c) = a*b + a*c
En el espacio vectorial de los marrones esto se enuncia de la siguiente forma:
"Si se distribuye un marrón de amplitud A entre dos sujetos pasivos b y c, el
resultado es que cada uno de ellos se come un marrón por lo menos igual de grande que el
original"
Corolario: (teoría del reparto del trabajo)
"Dado un marrón de amplitud A y n comemarrones, al producirse una
multiplicación de marrones teniendo en cuenta el número de sujetos pasivos se generarán
n marrones cuya intensidad varía de A a n*A."
Otras notas de interés
Nótese que no se definen las operaciones de resta ni de división
de marrones. Esto es normal ya que por su propia definición un marrón no puede restarse
de otro.
Además la división de marrones nunca es posible. En todo caso se puede dar una
multiplicación con la propiedad distributiva respecto de la suma.
|


